|
The flattop window is explicitly designed to avoid the picket fence effect. One situation where this is useful is if you are trying to build a tracking filter out of an FFT. For example, if you have signal that changes in frequency (say the first order of a rotating machine), and you want to track that signals amplitude as a function of time, the flattop window will give you the most accurate results.
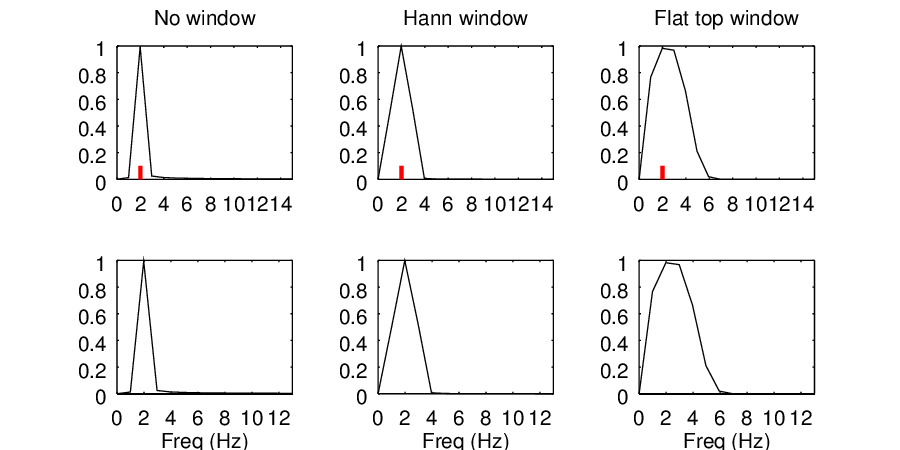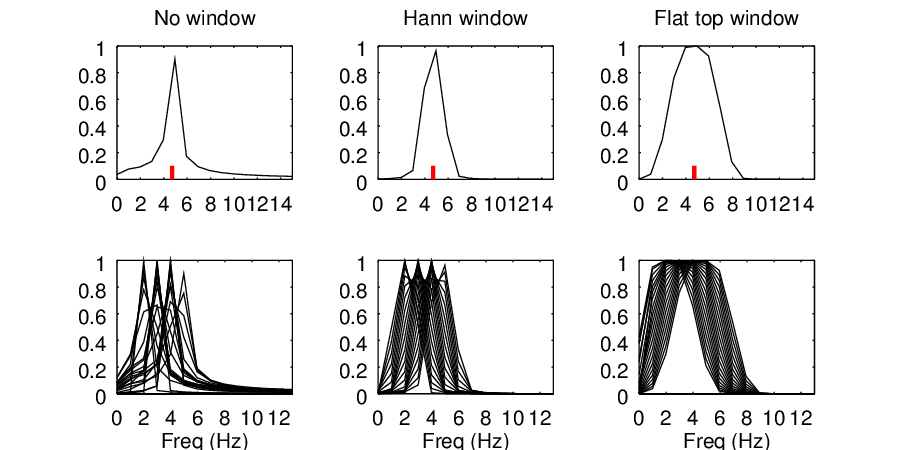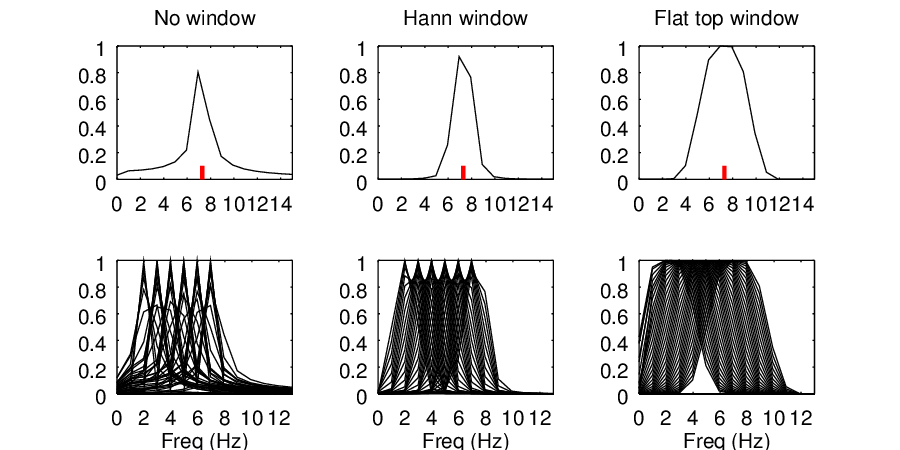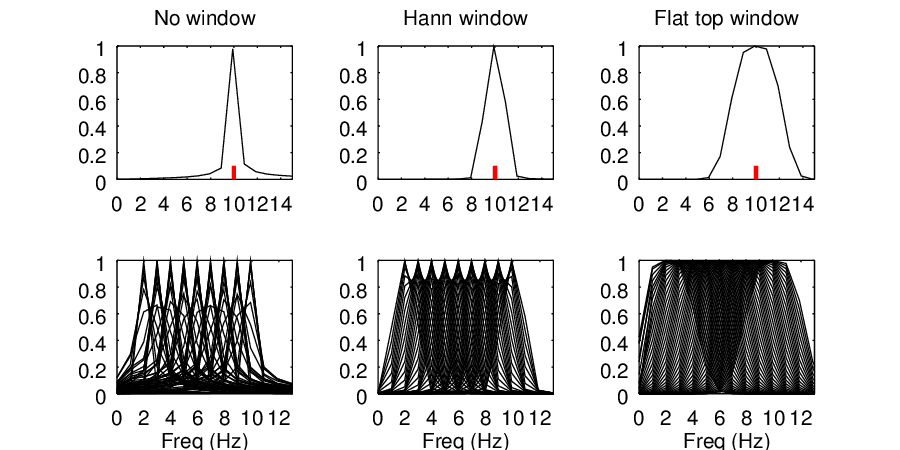
The figure below repeats the frequency sweep of section, 6.4.2 except with two different windows compared. You can see that the flat top window always has at least one bin with an amplitude that is very close to the true signal amplitude of 1.0. However, the price that you pay for this is a significantly wider frequency response.
Examination of the shape of the flat top window in figure 21 shows why the frequency response is wider. The window is very close to 0 for nearly two-thirds of the sample. Thus, the effective sample length is nearly 1/3 of the actual sample length, and so the effective bin width is nearly 3 times the actual bin width.

|
